Случайная величина — это переменная, которая может принимать различные значения в зависимости от случайных событий. Законы распределения случайных величин описывают вероятность того, что случайная величина примет определенное значение или попадет в определенный диапазон.
Существует несколько основных типов законов распределения случайных величин. Нормальное распределение (или распределение Гаусса) является одним из самых распространенных. Оно имеет симметричную колоколообразную форму и характеризуется свойством, что большинство значений сосредоточены вокруг среднего значения. Нормальное распределение широко используется в статистике и вероятностной теории.
Еще одним основным типом закона распределения случайных величин является равномерное распределение. В этом случае вероятность всех значений в заданном диапазоне одинакова. Например, если случайная величина представляет собой бросок кубика, то вероятность выпадения каждой из шести граней равна 1/6.
Другим интересным примером закона распределения случайной величины является экспоненциальное распределение. Оно используется для моделирования времени между последовательными случайными событиями, такими как интервалы между звонками в центре коллективного обслуживания или временем между срабатываниями определенного устройства.
Понятие случайной величины
Случайные величины могут быть дискретными и непрерывными. Дискретные случайные величины принимают значения из конечного или счетного множества, например, число выпавших очков на игральной кости. Непрерывные случайные величины принимают значения из непрерывного интервала, например, время, потраченное на выполнение задания.
Для описания поведения случайной величины используются законы распределения, которые показывают вероятность принятия различных значений случайной величиной. Наиболее распространенными законами распределения являются равномерное, нормальное и экспоненциальное распределения.
Случайные величины являются основой для построения статистических моделей и анализа данных. Они позволяют описывать и предсказывать случайные явления и определять их характеристики, такие как среднее значение и дисперсия.
Важно отметить, что понятие случайной величины тесно связано с понятием вероятности. С помощью случайных величин можно моделировать и анализировать вероятностные события, такие как выпадение определенной комбинации на игральной кости или вероятность успеха в эксперименте.
| Тип случайной величины | Пример |
|---|---|
| Дискретная | Число выпадений шестерки на игральной кости |
| Непрерывная | Время, потраченное на выполнение задания |
Случайные величины и вероятность
Вероятность — это мера возможности или невозможности возникновения определенного события. Случайные величины позволяют нам выразить вероятность события в числовой форме. Например, если мы интересуемся вероятностью выпадения орла при подбрасывании монеты, мы можем ввести случайную величину X, которая принимает значение 1, если выпал орел, и значение 0, если выпала решка.
Основные типы случайных величин включают дискретные и непрерывные случайные величины. Дискретные случайные величины принимают только определенные значения с определенными вероятностями. Например, количество выпавших орлов при 10 подбрасываниях монеты. Непрерывные случайные величины, напротив, могут принимать любое значение в определенном интервале. Например, время ожидания на автобусной остановке.
Для описания законов распределения случайных величин используются статистические функции, такие как функция распределения и плотность вероятности. Функция распределения определяет вероятность того, что случайная величина примет значение меньше или равное определенному числу. Плотность вероятности, в свою очередь, определяет вероятность попадания случайной величины в определенный интервал значений.
Знание случайных величин и вероятности позволяет нам моделировать и анализировать различные случайные явления, такие как стохастические процессы, финансовые рынки, прогнозирование погоды и многое другое. Поэтому понимание основных типов и свойств случайных величин является важной задачей для всех, кто работает с вероятностными моделями и статистикой.
Математическое ожидание случайной величины
Математическое ожидание обозначается символом МО и часто называется средним значением. Формально оно вычисляется, умножая каждое значение случайной величины на вероятность его появления и суммируя полученные произведения:
МО = x1P(x1) + x2P(x2) + … + xnP(xn)
Где x1, x2, …, xn – значения случайной величины, а P(x1), P(x2), …, P(xn) – вероятности их появления.
Математическое ожидание может принимать дискретные значения (если случайная величина имеет конечное или счетное число значений) или непрерывные значения (если случайная величина принимает значения на непрерывном интервале).
Математическое ожидание случайной величины может помочь в оценке ожидаемой прибыли или убытка, в планировании бюджета или контроле рисков в финансовой сфере, а также во многих других областях, где необходимо оценить среднее значение случайного явления.
Основные типы законов распределения случайных величин
Основные типы законов распределения случайных величин включают в себя:
| Тип распределения | Описание | Примеры |
|---|---|---|
| Нормальное распределение | Самое распространенное распределение, описывающее множество независимых случайных величин. Характеризуется симметричным колоколообразным графиком. Параметры распределения — математическое ожидание и дисперсия | Рост человека, измерение случайной ошибки |
| Биномиальное распределение | Используется для моделирования бинарных событий с определенной вероятностью успеха. Характеризуется двумя параметрами — количеством испытаний и вероятностью успеха | Результаты серии независимых экспериментов с двумя возможными исходами, такими как выпадение монеты |
| Равномерное распределение | Каждое значение в заданном диапазоне имеет одинаковую вероятность появления. Характеризуется двумя параметрами — минимальным и максимальным значением | Выбор случайного числа из интервала [a, b] |
| Экспоненциальное распределение | Используется для моделирования времени между последовательными событиями, такими как временные интервалы между двумя поступлениями заявок. Характеризуется одним параметром — средним временем между событиями | Время между поступлениями заявок на обслуживание |
| Пуассоновское распределение | Используется для моделирования числа событий, происходящих в заданном интервале времени или пространстве. Характеризуется одним параметром — интенсивностью событий | Количество покупок в магазине за определенный период времени |
Каждый из этих законов распределения имеет свои особенности, которые нужно учитывать при анализе данных и прогнозировании результатов. Знание основных типов законов распределения помогает улучшить качество статистического анализа и принимать более обоснованные решения.
Нормальное распределение
Нормальное распределение описывается плотностью вероятности, которая имеет форму симметричного колокола. Оно характеризуется двумя параметрами: математическим ожиданием (μ) и стандартным отклонением (σ). Математическое ожидание определяет положение пика колокола, а стандартное отклонение определяет его ширину. Чем больше значение стандартного отклонения, тем шире будет колокол и наоборот.
Вероятность попадания случайной величины в заданный интервал может быть вычислена с помощью интеграла от плотности вероятности. Под нормальной кривой площадь под графиком плотности вероятности равна 1.
Многие случайные величины в природе приближаются нормальным распределением. Примеры включают измерения физических величин, таких как рост и вес людей, а также результаты множества независимых случайных событий.
Нормальное распределение имеет много важных свойств, которые делают его очень полезным для анализа данных. Оно позволяет делать предсказания о вероятности того, что случайная величина попадет в определенный диапазон значений. Также нормальное распределение обладает свойством центральной предельной теоремы, которое гласит, что сумма большого числа независимых случайных величин имеет приближенно нормальное распределение.
| Параметр | Значение |
|---|---|
| Математическое ожидание (μ) | Любое действительное число |
| Стандартное отклонение (σ) | Положительное число |
| Формула плотности вероятности | f(x) = (1 / (σ√(2π))) * e^((-1/2)*((x — μ)/σ)^2) |
Биномиальное распределение
Биномиальное распределение имеет два параметра: количество испытаний n и вероятность успеха в каждом испытании p. Вероятность успеха и вероятность неудачи составляют единицу, то есть p + q = 1, где q = 1 — p.
Вероятность того, что в n испытаниях произойдет k успехов, задается биномиальным коэффициентом и может быть вычислена по формуле:
P(X = k) = C(n, k) * p^k * q^(n — k),
где C(n, k) — количество сочетаний из n по k, то есть число способов выбрать k успехов из n испытаний.
Биномиальное распределение имеет несколько основных свойств:
| Математическое ожидание | Дисперсия |
|---|---|
| E(X) = np | Var(X) = npq |
Биномиальное распределение широко применяется в различных сферах, таких как биология, медицина, экономика и др. Оно может использоваться для моделирования вероятности успеха или неудачи в серии независимых испытаний.
Равномерное распределение
Математически равномерное распределение описывается функцией плотности вероятности:
f(x) = 1 / (b — a), где a ≤ x ≤ b
где a и b – границы интервала значений случайной величины. Чтобы вычислить вероятность попадания случайной величины в заданный интервал [c, d], необходимо вычислить интеграл от функции плотности вероятности в этом интервале:
P(c ≤ x ≤ d) = ∫[c, d] f(x) dx = 1 / (b — a) ∫[c, d] dx = (d — c) / (b — a)
Таким образом, вероятность попадания случайной величины в любой интервал равна длине этого интервала, деленной на длину всего отрезка значений.
Примером применения равномерного распределения может быть моделирование случайного выбора числа от 1 до 10. В данном случае интервал [1, 10] будет соответствовать области значений случайной величины, а вероятность выпадения каждого числа будет 1/10.
Примеры распределения случайных величин
Случайные величины могут быть распределены по различным законам вероятности. Вот некоторые примеры распределений случайных величин:
| Тип распределения | Описание | Примеры |
|---|---|---|
| Равномерное распределение | Вероятность каждого значения в заданном интервале равна | Монетка (орел или решка), игральная кость, рулетка |
| Нормальное (гауссово) распределение | Симметричное распределение вокруг среднего значения | Рост людей, ошибка измерений |
| Биномиальное распределение | Количество успехов в серии независимых экспериментов (два возможных исхода) | Броски монеты, результаты опроса (да/нет) |
| Пуассоновское распределение | Количество событий, произошедших в заданном промежутке времени или пространстве | Количество звонков в центре коллективного пользования за определенный период времени |
| Экспоненциальное распределение | Время между последовательными событиями в процессе Пуассона | Время между приходом пассажиров в автобусную остановку |
Это лишь некоторые из множества распределений случайных величин, с которыми сталкиваются в теории вероятностей и статистике. Каждое из этих распределений имеет свои особенности и применяется в различных областях.
Пример распределения погрешности измерений
При проведении измерений всегда возникает некоторая погрешность, связанная с неточностью используемых инструментов, влиянием окружающей среды и другими факторами. Для описания распределения этой погрешности часто используется нормальное распределение.
Нормальное распределение характеризуется симметричностью относительно среднего значения и формой колокола. Математическое ожидание и стандартное отклонение определяют форму и разброс распределения, а плотность вероятности позволяет оценить вероятность значения в определенном диапазоне.
Например, представим, что мы провели измерение длины некоторого объекта и получили следующие результаты: 10, 11, 9, 10.5, 10.2. Очевидно, что неточность при измерении может привести к разным результатам, даже если объект имеет фиксированную длину.
Рассчитав среднее значение (10.14) и стандартное отклонение (0.57) для этих измерений, мы можем оценить вероятность получить конкретное значение или диапазон значений. Например, вероятность измерить длину в пределах от 9 до 11 будет равна площади под кривой нормального распределения в этом диапазоне.
Таким образом, нормальное распределение позволяет описывать и анализировать погрешности измерений, делая возможным определение допустимых диапазонов значений и проведение статистического анализа результатов измерений.
Вопрос-ответ:
Какие существуют основные типы распределения случайных величин?
Существует несколько основных типов распределения случайных величин. Некоторые из них включают равномерное распределение, нормальное распределение, биномиальное распределение, распределение Пуассона и геометрическое распределение.
Что такое равномерное распределение?
Равномерное распределение — это тип распределения случайных величин, при котором вероятность получения любого значения в диапазоне значений одинакова. Например, если бросать правильную кубическую кость, вероятность выпадения каждого числа от 1 до 6 будет одинаковой.
Как можно описать нормальное распределение?
Нормальное распределение, также известное как распределение Гаусса, является одним из самых распространенных типов распределения случайных величин. Оно характеризуется колоколообразной формой графика вероятностей, где большинство значений сконцентрировано вокруг среднего значения, а значения на краях графика реже встречаются.
Какими примерами можно описать биномиальное распределение?
Биномиальное распределение применяется в случаях, когда проводится серия независимых испытаний, каждое из которых имеет два возможных исхода: успех или неудача. Например, бросание монетки или выборка случайных людей, где можно задать вопрос с двумя возможными ответами. Еще одним примером является распределение числа людей, сдавших экзамен, при условии некоторой вероятности успеха.
Каким образом задаётся распределение Пуассона?
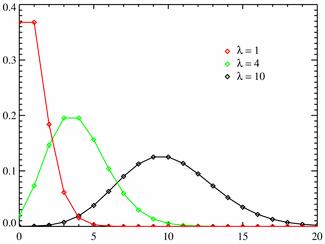
Распределение Пуассона используется для моделирования числа редких событий в определенном периоде времени или пространстве. Оно описывается одним параметром — средним значением числа событий, происходящих в заданном интервале. Примерами могут служить число звонков, поступающих в службу скорой помощи за определенный промежуток времени, или число опечаток на странице газеты.
Какие основные типы законов распределения случайных величин?
Основные типы законов распределения случайных величин включают непрерывные и дискретные распределения. Непрерывные распределения описывают случайные величины, которые могут принимать любое значение в определенном интервале, такие как равномерное распределение или нормальное распределение. Дискретные распределения, напротив, описывают случайные величины, которые принимают только конкретные значения, такие как распределение Пуассона или биномиальное распределение.
Какие примеры непрерывных распределений случайных величин?
Примеры непрерывных распределений случайных величин включают равномерное распределение, нормальное распределение, экспоненциальное распределение и гамма-распределение. Равномерное распределение характеризуется равной вероятностью для каждого значения в определенном интервале. Нормальное распределение, или распределение Гаусса, является одним из наиболее распространенных типов распределений и имеет колоколообразную форму. Экспоненциальное распределение моделирует время между двумя последовательными событиями, а гамма-распределение обобщает экспоненциальное распределение и может быть использовано для моделирования времени ожидания нескольких событий.