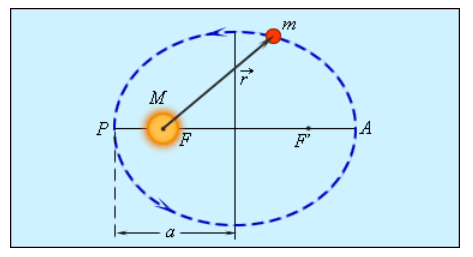
Закон Кеплера 3, также известный как закон радиус-вектора, является одной из трех основных законов движения планет вокруг Солнца. Он был открыт немецким астрономом Иоганном Кеплером в начале 17 века и стал одним из фундаментальных принципов астрономии.
Формула закона Кеплера 3 выражает зависимость между периодом обращения планеты вокруг Солнца и средним расстоянием этой планеты от Солнца. Согласно закону, квадрат периода обращения планеты (T) прямо пропорционален кубу ее большой полуоси (a): T^2 = k * a^3.
Этот закон помогает понять, что скорость обращения планеты вокруг Солнца меняется в зависимости от ее расстояния от него. Более удаленные планеты имеют большие периоды обращения и меньшие скорости, тогда как ближайшие планеты движутся быстрее и имеют более короткие периоды обращения.
Формула закона Кеплера 3
Третий закон Кеплера устанавливает связь между периодом обращения планеты вокруг Солнца и её средним расстоянием до Солнца. Формула этого закона выглядит следующим образом:
T^2 = k * R^3
Где:
- T — период обращения планеты вокруг Солнца (время, затраченное на один полный оборот);
- R — среднее расстояние планеты до Солнца;
- k — постоянная, зависящая от массы Солнца.
Эта формула позволяет вычислить период обращения планеты вокруг Солнца, если известно её среднее расстояние до Солнца, и наоборот.
Обратная связь: Кубическая компонента
Закон Кеплера 3 описывает движение небесных тел по орбите вокруг центрального объекта. Он утверждает, что квадрат периода обращения планеты вокруг Солнца пропорционален кубу ее большой полуоси:
T^2 = k * a^3
где T — период обращения планеты вокруг Солнца, a — большая полуось орбиты планеты, k — постоянная пропорциональности.
Таким образом, если мы знаем период обращения и большую полуось орбиты, мы можем вычислить постоянную пропорциональности и, следовательно, использовать эту формулу для предсказания периода обращения других планет или небесных тел.
Обратная связь: кубическая компонента закона Кеплера 3 представляет собой отношение куба большой полуоси орбиты одного небесного тела к кубу большей полуоси орбиты другого небесного тела:
(a1/a2)^3 = (T1/T2)^2
где a1 и a2 — большие полуоси орбиты двух небесных тел, T1 и T2 — их периоды обращения соответственно.
Таким образом, зная большие полуоси и периоды обращения двух небесных тел, мы можем использовать обратную связь: кубическую компоненту для определения отношения между ними.
Период орбиты: Квадратная компонента
Как известно, закон Кеплера 3 гласит, что квадрат периода обращения планеты (T) пропорционален кубу большой полуоси ее орбиты (a):
T^2 = k \cdot a^3,
где k — постоянная, зависящая от массы центрального тела.
Период орбиты представляет собой время, за которое планета совершает полный оборот вокруг центрального тела. Он измеряется в единицах времени (например, в секундах, минутах или годах).
Квадратная компонента закона Кеплера 3 говорит о том, что период орбиты планеты зависит от большой полуоси ее орбиты, возведенной в куб.
Можно использовать данную формулу для определения периода обращения планеты вокруг центрального тела, если известны его масса и большая полуось орбиты. Это позволяет проводить расчеты и предсказывать движение планет с высокой точностью.
| Символ | Обозначение | Единицы измерения |
|---|---|---|
| T | Период орбиты | секунды, минуты, часы, дни, годы и т.д. |
| a | Большая полуось орбиты | метры, километры, астрономические единицы и т.д. |
Таким образом, квадратная компонента закона Кеплера 3 дает нам инструмент для изучения и прогнозирования движения планет вокруг центрального тела.
Объяснение закона Кеплера 3
Закон Кеплера 3 также известен как «закон радиусов». Он гласит, что квадраты периодов обращения планет вокруг Солнца пропорциональны кубам их средних расстояний до Солнца.
Этот закон является одним из трех законов Иоганна Кеплера, которые помогли установить основы классической механики и позволили Ньютону сформулировать законы движения и гравитацию.
Закон Кеплера 3 можно сформулировать математически следующим образом:
T2 ∝ R3
Где:
- T — период обращения планеты вокруг Солнца
- R — среднее расстояние планеты до Солнца
То есть, квадрат периода обращения планеты пропорционален кубу ее среднего расстояния до Солнца. Другими словами, чем дальше планета находится от Солнца, тем дольше ей требуется для завершения одного оборота вокруг него.
Закон Кеплера 3 помогает объяснить, почему планеты, находящиеся ближе к Солнцу, имеют более короткие периоды обращения, а планеты, находящиеся дальше, имеют более длинные периоды обращения.
Этот закон имеет важное прикладное значение при расчете орбит спутников, планет и других небесных тел. Он также помогает установить закономерности в движении небесных объектов и понять структуру Солнечной системы.
Гравитационные силы и расстояние
Гравитационные силы между двумя телами зависят от их масс и расстояния между ними. Как только расстояние между телами увеличивается, гравитационная сила между ними уменьшается. Это можно объяснить принципом обратно пропорциональности.
Формула для расчета гравитационной силы выглядит следующим образом:
F = G * ((m1 * m2) / r^2)
где F — гравитационная сила, G — гравитационная постоянная, m1 и m2 — массы двух тел, r — расстояние между ними.
Эта формула позволяет определить силу, которая действует между двумя телами на определенном расстоянии.
Применение закона Кеплера 3 особенно полезно в астрономии. Например, позволяет определить период обращения планет вокруг Солнца или спутников вокруг планеты и предсказать будущие положения планет и спутников.
Также, этот закон является основой для понимания многих физических явлений и применяется в различных исследованиях и технологиях, например, в космической навигации и расчете орбит и путей движения искусственных спутников.
Скорость планет при движении по орбите
Основная формула, объясняющая связь между скоростью планеты и её дистанцией до Солнца, выглядит следующим образом:
v = 2πa / T
Где v — скорость планеты, a — среднее расстояние между планетой и Солнцем (длина большой полуоси её орбиты), T — период обращения планеты вокруг Солнца.
Из этой формулы следует, что скорость планеты при движении по орбите зависит от её дистанции до Солнца. Чем дальше планета находится от Солнца, тем меньше её скорость, а чем ближе — тем больше. Например, Земля, находящаяся на среднем расстоянии около 150 миллионов километров от Солнца, имеет скорость около 30 км/с.
Скорость планеты может изменяться на протяжении всей её орбиты. Наибольшую скорость планета достигает в точке орбиты, ближайшей к Солнцу, называемой перигелием. В точке орбиты, наиболее удалённой от Солнца, называемой афелием, скорость планеты минимальна.
Знание скорости планеты позволяет исследователям астрономии более глубоко изучать движение планет в Солнечной системе и их взаимодействие с другими небесными объектами. Также скорость играет важную роль при планировании и осуществлении космических миссий и космических полётов.
Применение закона Кеплера 3
Применение закона Кеплера 3 позволяет астрономам определить орбитальные характеристики различных небесных тел. Это особенно важно при изучении систем планет. Знание периода обращения планет вокруг своей звезды позволяет астрономам определить такие характеристики, как массы планет и звезды, а также расстояние между ними.
Применив закон Кеплера 3, ученые могут также вычислить массу и плотность планеты, пользуясь информацией о периоде орбиты спутников, а также определить структуру и состав планеты. Это позволяет более подробно изучать планетарные системы и разрабатывать модели их эволюции.
Закон Кеплера 3 также находит применение при изучении движения источников света, таких как звезды или галактики. Путем измерения периода изменения светимости или частоты излучения таких объектов и зная расстояние до них, можно определить их массу и другие характеристики.
Информация, полученная с помощью применения закона Кеплера 3, позволяет ученым лучше понять законы природы и улучшить наши знания о Вселенной. Она также открывает новые возможности для изучения искусственных спутников, астронавтики и дальнейшего исследования космоса.
Расчеты орбитальных параметров планет
- Период обращения – это время, за которое планета совершает полный оборот вокруг Солнца. Для расчета периода обращения достаточно знать радиус орбиты планеты и массу Солнца. Период обращения можно вычислить по формуле:
T = 2 * pi * sqrt(a^3 / GM),
гдеT— период обращения,pi— число Пи,a— радиус орбиты планеты иGM— гравитационная постоянная, равная произведению массы Солнца на гравитационную постоянную:GM = G * MS, гдеG— гравитационная постоянная, аMS— масса Солнца. - Скорость планеты – это скорость, с которой планета движется по своей орбите. Скорость планеты можно вычислить по формуле:
V = sqrt(GM / a),
гдеV— скорость планеты. - Эксцентриситет орбиты – это мера отклонения орбиты планеты от формы окружности. Эксцентриситет можно рассчитать по формуле:
e = sqrt(1 - (b^2 / a^2)),
гдеe— эксцентриситет орбиты,a— большая полуось орбиты, аb— малая полуось орбиты. - Аргумент перицентра – это угол между линией апсид и перицентром орбиты планеты. Апсид – это точка орбиты, ближайшая к Солнцу, а перицентр – точка орбиты, наиболее удаленная от Солнца. Аргумент перицентра можно вычислить по формуле:
w = atan2(y, x),
гдеw— аргумент перицентра,y— вертикальная координата перицентра, аx— горизонтальная координата перицентра. - Время пролета перицентра – это время, через которое планета достигнет перицентра после прошлого прохождения перицентра. Время пролета перицентра можно вычислить по формуле:
Tp = T * (Mm - Mi) / (2 * pi),
гдеTp— время пролета перицентра,T— период обращения планеты,Mm— средняя аномалия планеты на момент прохождения перицентра, аMi— средняя аномалия планеты на момент предыдущего прохождения перицентра.
Рассчитывая орбитальные параметры планет, мы можем лучше понять и предсказать их движение вокруг Солнца. Эти расчеты имеют важное значение в астрономических и космических исследованиях.
Определение перемещений планет на орбите
Согласно Закону Кеплера 3, квадрат периода обращения планеты вокруг Солнца пропорционален кубу большой полуоси орбиты планеты. То есть, T^2 ∝ a^3, где T — период обращения планеты, а — большая полуось ее орбиты.
Для применения Закона Кеплера 3 необходимо знать период обращения планеты и большую полуось ее орбиты. Период обращения можно найти, изучая движение планеты в течение некоторого времени. Большую полуось орбиты можно определить из данных о расстоянии планеты от Солнца, которые получены при помощи специальных измерительных приборов.
Используя формулу Закона Кеплера 3, астрономы могут определить перемещения планет на их орбитах, а также предсказывать положение планеты в будущем. Это позволяет уточнить расчеты орбит и строить более точные космические миссии.
Вопрос-ответ:
Как можно описать закон Кеплера 3?
Закон Кеплера 3 гласит о том, что квадрат периода обращения планеты вокруг Солнца пропорционален кубу её среднего расстояния до Солнца.
Какая формула используется для закона Кеплера 3?
Формулой для закона Кеплера 3 является следующая: T^2 = k * r^3, где T — период обращения планеты вокруг Солнца, r — среднее расстояние планеты до Солнца, а k — постоянная, зависящая от массы Солнца и выбранной единицы измерения.
Как можно объяснить закон Кеплера 3?
Закон Кеплера 3 объясняется гравитационным взаимодействием между планетами и Солнцем. Планета движется по эллиптической орбите вокруг Солнца, при этом гравитационная сила, действующая на планету, обратно пропорциональна квадрату расстояния до Солнца. Это приводит к тому, что период обращения планеты возрастает с увеличением её расстояния от Солнца.
Как можно применить закон Кеплера 3 в практической деятельности?
Закон Кеплера 3 позволяет установить зависимость между периодом обращения планеты вокруг Солнца и её расстоянием до Солнца. Это позволяет использовать закон для расчёта периодов обращения планет и астероидов, а также для нахождения их расстояний от Солнца. Также закон Кеплера 3 используется в астрономии для изучения движения планет и астероидов в Солнечной системе.
Какую роль играет закон Кеплера 3 в понимании космических явлений?
Закон Кеплера 3 является одним из основных законов, позволяющих понять и описать движение планет и астероидов в Солнечной системе. Он помогает установить зависимость между периодом обращения планет и их расстоянием от Солнца, что позволяет лучше понять строение и эволюцию нашей Солнечной системы. Также данный закон играет важную роль в поисках и изучении экзопланет — планет, находящихся вокруг других звезд.
Какая основная идея, лежащая в основе Закона Кеплера 3?
Закон Кеплера 3 утверждает, что квадраты периодов обращения планет вокруг Солнца пропорциональны кубам больших полуосей их орбит.
Как проиллюстрировать Закон Кеплера 3 на примере Земли?
Например, если мы возьмем Землю, то ее орбита является эллипсом, а период обращения вокруг Солнца составляет примерно 365 дней. Если мы возведем это число в квадрат, то получим около 133225 дней. А если возведем большую полуось орбиты Земли в куб, то получим около 166376870000 кубических километров. Оказывается, что эти два значения практически идентичны, что подтверждает Закон Кеплера 3.