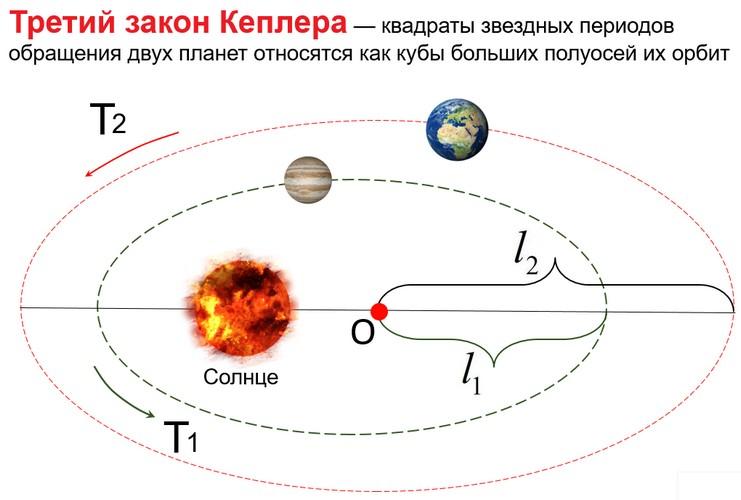
В астрономии одна из основных задач – изучение движения небесных тел. Одним из наиболее важных законов, описывающих движение планет вокруг Солнца, является закон Кеплера 2, который устанавливает, что площадь, заметаемая радиус-вектором планеты за равное время, постоянна. Это означает, что при движении вокруг Солнца планета равные участки пути заметает за равные промежутки времени. Но какова формула этого закона и какое значение он имеет в астрономии?
Закон Кеплера 2 можно выразить математической формулой:
A/T = const,
где A – площадь, заметаемая радиус-вектором планеты, а T – время, за которое планета проходит равные участки орбиты.
Значение закона Кеплера 2 заключается в том, что он позволяет определить закономерности движения планет и спутников вокруг центрального тела. Это значительно облегчает астрономические расчеты и позволяет прогнозировать положение планеты в будущем. Знание этого закона является одним из основных фундаментальных принципов астрономии.
Значение закона Кеплера 2 в астрономии
Закон Кеплера 2, также известный как закон радиус-векторов, формулирует связь между периодами обращения планет вокруг Солнца и их средними расстояниями от Солнца. Согласно этому закону, квадрат периода обращения планеты пропорционален кубу ее среднего расстояния от Солнца.
Формула закона Кеплера 2 выражается следующим образом:
T2 = k * r3
Где:
- T — период обращения планеты вокруг Солнца.
- k — постоянная, зависящая от массы Солнца и выбранной системы единиц измерения.
- r — среднее расстояние планеты от Солнца.
Закон Кеплера 2 играет важную роль в астрономии, поскольку позволяет устанавливать зависимость между периодами обращения планет и их орбитальными характеристиками. Этот закон был открыт и сформулирован немецким астрономом Йоганном Кеплером в 17 веке на основе наблюдений и анализа данных орбитальных движений планет.
С помощью закона Кеплера 2 астрономы могут определить среднее расстояние планет от Солнца, исходя из известного периода их обращения. Он помогает установить характеристики орбит, включая эксцентриситет и угол наклона.
Закон Кеплера 2 также позволяет проводить сравнительный анализ планетарных систем и исследовать их эволюцию и формирование. Астрономы используют его для изучения распределения планет в различных зонаках внешней и внутренней области звездных систем.
Формула Закона Кеплера 2
Закон Кеплера 2, также известный как закон равности площадей, устанавливает связь между периодом обращения планеты вокруг Солнца и её большой полуосью орбиты. Формула, которая описывает этот закон, выглядит следующим образом:
T2 = k * a3
где:
- T — период обращения планеты вокруг Солнца (измеряемый в единицах времени, например, годах);
- k — постоянная, которая имеет одно и то же значение для всех планет Солнечной системы;
- a — большая полуось орбиты планеты (измеряемая в единицах длины, например, астрономических единицах).
Формула Закона Кеплера 2 позволяет определить период обращения планеты вокруг Солнца, исходя из её большой полуоси орбиты. Это наблюдаемое равенство площадей позволяет формализовать закон равных площадей, установленный Иоганном Кеплером в 17 веке. Формула имеет большое значение в астрономии и позволяет ученым изучать движение планет и других тел в Солнечной системе, а также предсказывать их положение в будущем.
Формула для расчёта периода вращения планеты вокруг Солнца
Период вращения планеты вокруг Солнца определяется размером орбиты и массой Солнца. Формула для расчёта периода выглядит следующим образом:
Tпериод = 2π × (√(a3 / G × MСолнца))
Где:
- Tпериод — период вращения планеты вокруг Солнца;
- π — математическая константа, примерно равная 3.14159;
- a — большая полуось орбиты планеты;
- G — гравитационная постоянная, примерно равная 6.67 × 10-11 м3/(кг × c2);
- MСолнца — масса Солнца.
Зная значения большой полуоси орбиты и массы Солнца, можно вычислить период вращения планеты вокруг Солнца с использованием данной формулы. Это позволяет астрономам лучше понять и изучить движение планет и других небесных тел в нашей Солнечной системе.
Формула в математической форме
Закон Кеплера 2 можно записать в математической форме следующим образом:
Т^2 = к^3 * (4π^2 / G * М) * (a^3 / R^2)
- Т — период обращения планеты вокруг Солнца
- к — постоянная, зависящая от вида орбиты (1 для круговой орбиты и отличная от 1 для эллиптической орбиты)
- π — число Пи, примерно равное 3,14159
- G — гравитационная постоянная
- М — масса Солнца
- a — большая полуось орбиты планеты
- R — расстояние между Солнцем и планетой
Эта формула позволяет определить период обращения планеты вокруг Солнца с помощью известных параметров, таких как масса Солнца, большая полуось орбиты и расстояние до Солнца. Формула имеет важное значение в астрономии, поскольку позволяет определить периоды обращения планет и даже спутников вокруг других небесных тел. Это позволяет уточнить наши знания о движении небесных объектов и структуре вселенной.
Значение формулы в астрономии
Закон Кеплера 2, выраженный в форме математической формулы, играет важную роль в астрономических исследованиях. Данная формула позволяет установить связь между периодом обращения планеты вокруг Солнца и средним расстоянием до Солнца.
Закон Кеплера 2 формализует следующую зависимость:
| Период обращения планеты (T) | = | 2π * квадратный корень из (среднее расстояние до Солнца (a))^3 |
Данная формула позволяет астрономам определить период обращения планеты вокруг Солнца по известному среднему расстоянию до Солнца, и наоборот. Это важно для составления орбитальных карт планет и понимания их движения. Кроме того, данная формула является основой для решения различных задач, связанных с орбитальной механикой и астрономией в целом.
Применение Закона Кеплера 2 в астрономии
Закон Кеплера 2 гласит, что планеты движутся по эллиптическим орбитам вокруг Солнца, в одном из фокусов орбиты, причем площади, заметаемые радиус-вектором планеты за равные интервалы времени, пропорциональны. Математически это выражается следующей формулой:
T2 = a3,
где T — период обращения планеты вокруг Солнца (в секундах, минутах, часах или годах), а — большая полуось орбиты планеты (в километрах, астрономических единицах или световых годах).
Этот закон был сформулирован Кеплером на основе точных наблюдений планет движущихся вокруг Солнца, и его значимость заключается в том, что он позволяет установить связь между временем обращения планеты вокруг Солнца и её орбитальными параметрами, такими как её полуосью. Это позволяет астрономам определять орбиты планет и других небесных тел, и использовать эти данные для более глубокого понимания механизмов движения в космосе.
Применение Закона Кеплера 2 позволяет уточнить орбитальные параметры планет и спутников, а также предсказывать их движение в будущем. Например, используя этот закон, астрономы могут составить точные таблицы и эфемериды движения планет, которые необходимы для планирования космических миссий или астрономических наблюдений.
Кроме того, Закон Кеплера 2 оказал большое влияние на развитие астрономии и физики в целом. Он служит основой для понимания движения не только планет, но и других небесных тел, таких как кометы, спутники и даже галактики. Благодаря этому закону ученые могут вычислять массы планет и звезд, и изучать различные процессы, происходящие во Вселенной.
Определение планеты по её орбитальному периоду
Кеплер в своих законах движения планет показал, что орбитальный период планеты связан со средним расстоянием до своей звезды. Он получил формулу, которая описывает эту зависимость:
T2 = k*a3
Где T — орбитальный период планеты, a — среднее расстояние до своей звезды, k — постоянная, зависящая от массы звезды и измеряемая в годах и астрономических единицах.
Используя эту формулу, астрономы могут определить массу планеты, исходя из её орбитального периода и среднего расстояния до звезды. Это очень важно для изучения и классификации экзопланет, то есть планет, которые находятся за пределами Солнечной системы.
Важно отметить, что определение планеты по её орбитальному периоду является только одним из способов и требует дополнительных наблюдений и измерений для более точных результатов. Однако он является важным шагом в изучении и понимании тайн вселенной и её составляющих.
Вопрос-ответ:
Какая формула описывает второй закон Кеплера?
Формула, которая описывает второй закон Кеплера, называется «закон периодов». Она гласит, что квадраты периодов обращения планет вокруг Солнца пропорциональны кубам больших полуосей их орбит.
Каким образом второй закон Кеплера используют в астрономии?
Второй закон Кеплера используется в астрономии для определения орбитальных параметров планет и других небесных тел. Он позволяет оценить их периоды обращения и расстояния от Солнца.
Какое значение имеет второй закон Кеплера для понимания движения планет?
Второй закон Кеплера имеет важное значение для понимания движения планет. Он позволяет установить, что планеты движутся по эллиптическим орбитам вокруг Солнца и что скорость их движения не постоянна во все время обращения.
Какое значение имеет второй закон Кеплера для развития космических исследований?
Второй закон Кеплера имеет важное значение для развития космических исследований, так как он позволяет предсказывать и определять траектории и перемещения космических аппаратов в системе Солнечной системы и других планетных системах.
Какова история открытия второго закона Кеплера?
Второй закон Кеплера был открыт немецким астрономом Иоганном Кеплером в начале XVII века. Он проводил многолетние наблюдения планет и Солнечной системы и пришел к выводу о том, что планеты движутся по эллиптическим орбитам и меняют скорость движения в зависимости от своего положения на орбите.
Какая формула закона Кеплера 2 и каково её значение в астрономии?
Формула закона Кеплера 2 гласит, что квадрат периода обращения планет вокруг Солнца пропорционален кубу большой полуоси их орбиты. Значение формулы закона Кеплера 2 очень важно для астрономии, так как позволяет предсказывать и изучать орбитальные характеристики планет и других небесных объектов.