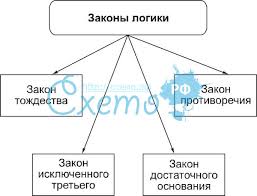
Среди основных логических законов можно выделить следующие:
1. Закон исключенного третьего: каждое утверждение может быть либо истинным, либо ложным. Нет третьего варианта. Например, утверждение «сегодня солнечно» или «сегодня не солнечно» истинно или ложно.
2. Закон противоречия: невозможно, чтобы оба утверждения, стоящие в противоположной зависимости друг от друга, были одновременно истинными. Например, утверждение «я пью чай» и «я не пью чай» не могут быть одновременно истинными.
3. Закон двойного отрицания: если мы дважды отрицаем какое-либо утверждение, то мы получаем утверждение, эквивалентное исходному. Например, «он не знает ничего» эквивалентно «он знает все».
4. Закон связи понятий: любой предмет может быть отнесен либо к какому-то классу, либо не отнесен ни к одному классу. Например, предмет «яблоко» либо относится к классу «фрукты», либо не относится ни к одному классу (например, к классу «животные»).
Навык применения основных логических законов помогает нам стать более аргументированными и рациональными в нашем мышлении. Понимание этих законов помогает нам строить логические цепочки рассуждений и доказывать свои утверждения. Логические законы являются основой для многих других логических анализов и размышлений, поэтому их изучение имеет огромное значение для развития нашего мышления.
Изучаем основные логические законы
Закон идемпотентности гласит, что если утверждение истинно, то оно остается истинным при повторном применении. Например, если «A» истинно, то «A и A» также истинно.
Закон противоречия устанавливает, что не может существовать одновременно истинное и ложное утверждение. То есть, в одном и том же контексте «A» и «не A» не могут быть одновременно истинными.
Закон исключенного третьего гласит, что в любом утверждении либо истина, либо ложь. То есть, утверждение либо «A» истинно, либо «A» ложно.
Закон двойного отрицания устанавливает, что двойное отрицание любого утверждения дает первоначальное утверждение. Например, если «A» является истинным, то «не (не A)» также является истинным.
Знание и применение логических законов помогает нам становиться более аналитически мыслящими и принимать обоснованные решения на основе логического рассуждения.
Виды логических законов
Логические законы представляют собой всеобщие принципы, которые определяют поведение логических операций и связей между ними. Существует несколько основных видов логических законов.
- Закон тождества (закон идентичности): данный закон утверждает, что если выражение равно самому себе, то оно всегда является истинным. То есть, A = A. Например, высказывание «Солнце встает каждое утро» всегда будет являться истиной.
- Закон противоречия: сущность этого закона заключается в том, что невозможно, чтобы одновременно истинными были и утверждение, и его отрицание. Например, высказывания «Сегодня понедельник» и «Сегодня не понедельник» не могут быть одновременно верными.
- Закон исключенного третьего: данный закон утверждает, что для любого утверждения и его отрицания существует только два возможных варианта: либо одно из высказываний истинно, либо оба являются ложными. Например, высказывания «Сегодня праздник» и «Сегодня не праздник» не могут быть одновременно ложными.
- Закон импликации: данный закон выражает связь между условием и его последствием. Если условие истинно, то и последствие также является истинным. Например, если «Если идет дождь, то улицы мокрые», то при наличии дождя улицы будут мокрыми.
- Закон коммутативности: этот закон говорит о том, что порядок операций не влияет на результат. Например, если «А и В» истинно, то и «В и А» также будет истинно.
Это лишь некоторые примеры логических законов, которые широко используются в математике, философии и информатике. Знание и понимание этих законов помогает производить анализ и рассуждения на основе логических принципов.
Законы идемпотентности
Одним из важных принципов математической логики является закон идемпотентности. Согласно этому закону, если применить определенную операцию к некоторому значению или состоянию дважды, результат будет идентичен применению этой операции один раз.
Существуют два основных закона идемпотентности:
- Закон двойного отрицания: значение, полученное путем двойного отрицания некоторого утверждения, эквивалентно исходному утверждению. Например, если утверждение «сегодня солнечный день» верно, то утверждение «сегодня несолнечный день» будет также истинным.
- Закон идемпотентности конъюнкции и дизъюнкции: результат конъюнкции (логического И) или дизъюнкции (логического ИЛИ) значения с самим собой будет эквивалентен исходному значению. Например, если утверждение «сегодня дождь» верно, то утверждения «сегодня дождь или дождь» и «сегодня дождь и дождь» также будут истинными.
Законы идемпотентности широко используются в математической логике, программировании и теории множеств. Они позволяют упростить и анализировать сложные логические выражения и операции, облегчая работу с логическими значениями и утверждениями.
Важно помнить, что закон идемпотентности работает только для операций и операторов, которые являются идемпотентными. Для других видов операций и операторов применение закона идемпотентности не даст правильного результата.
Законы коммутативности
Закон коммутативности сложения: a + b = b + a
Закон коммутативности умножения: a * b = b * a
Эти два закона можно применять как в алгебре, так и в логике. Они указывают на возможность изменения порядка слагаемых или множителей без изменения результата операции. Например, в математике мы можем переставить слагаемые в сумме, и она останется равной.
В логике эти законы утверждают, что порядок операций «И» и «ИЛИ» не важен. Например, в выражении «A И B» можно поменять местами «A» и «B», и результат останется тем же.
Законы коммутативности играют важную роль в математических и логических рассуждениях, позволяя упрощать выражения и сравнивать их.
Законы ассоциативности
Существует три основных закона ассоциативности: ассоциативность в сложении, ассоциативность в умножении и ассоциативность в операциях логического «И» и логического «ИЛИ».
Закон ассоциативности в сложении гласит, что порядок складываемых чисел не влияет на результат, то есть (а + b) + c = a + (b + c). Например, сумма чисел 2, 3 и 4 будет такой же, независимо от порядка их сложения: (2 + 3) + 4 = 2 + (3 + 4) = 9.
Закон ассоциативности в умножении утверждает, что порядок множителей не влияет на результат, то есть (a * b) * c = a * (b * c). Например, произведение чисел 2, 3 и 4 будет таким же, независимо от порядка их умножения: (2 * 3) * 4 = 2 * (3 * 4) = 24.
Закон ассоциативности в операциях логического «И» и логического «ИЛИ» утверждает, что порядок выполнения операций «И» и «ИЛИ» не влияет на их результат, то есть (p И q) И r = p И (q И r) и (p ИЛИ q) ИЛИ r = p ИЛИ (q ИЛИ r). Например, результат логической операции «И» будет таким же, независимо от порядка операндов: (true И false) И true = true И (false И true) = false.
Законы ассоциативности являются основой для выполнения логических операций и позволяют упростить их выполнение, а также облегчают анализ логических выражений.
Принципы логических законов
Вот некоторые из основных принципов логических законов:
| Принцип | Описание |
|---|---|
| Принцип тождества (Закон Идемпотентности) | Утверждение всегда равно самому себе. Если A — истина, то A = A. |
| Принцип исключенного третьего | Любое утверждение или является истинным (A), или является ложным (¬A). Нет третьего варианта. |
| Принцип неразличимости идентичных | Если A и B являются идентичными, то любое утверждение, содержащее A, может быть заменено на аналогичное утверждение, содержащее B. |
| Принцип противоречия | Утверждение не может быть одновременно истинным и ложным. Если A = истина, то ¬A = ложь. |
| Принцип достаточного основания | Любая логическая конструкция должна быть обоснована на основе иных логических законов или передачи информации. |
Применение принципов логических законов позволяет проводить рассуждения, доказывать и опровергать утверждения, а также строить последовательные логические цепочки.
Принцип невыполнимости
Принцип невыполнимости является противоположным принципу выполнимости, который утверждает, что существуют значения переменных, при которых логическое выражение становится истинным.
Для более наглядного представления принципа невыполнимости часто используется таблица истинности, которая показывает все возможные комбинации значений переменных и соответствующие им значения логического выражения.
| Переменная A | Переменная B | Логическое выражение |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Из представленной таблицы видно, что независимо от значений переменных A и B, логическое выражение всегда принимает значение 0 (ложное). Таким образом, данное выражение является невыполнимым.
Принцип невыполнимости играет важную роль при анализе и оптимизации логических выражений. Он позволяет определить, что на основании заданных условий невозможно достичь определенного результата, что может быть полезно при проектировании программного обеспечения.
Вопрос-ответ:
Какие основные логические законы существуют?
Основные логические законы включают в себя закон исключённого третьего, закон противоречия, и закон двойного отрицания.
Что означает закон исключённого третьего?
Закон исключённого третьего гласит, что для каждого утверждения либо оно истинно, либо его отрицание истинно.
Можно ли привести пример закона исключённого третьего?
Да, например, утверждение «Сегодня день» либо истинно, либо ложно. Нет третьего варианта.
Каким образом проявляется закон противоречия?
Закон противоречия гласит, что нельзя, чтобы одновременно было и истинное, и ложное утверждение.
Как можно применить закон двойного отрицания?
Закон двойного отрицания утверждает, что двойное отрицание истинное утверждение эквивалентно самому утверждению. Например, если сказать «Он не плохой», это эквивалентно утверждению «Он хорош».
Какие существуют основные логические законы?
Существует три основных логических закона: закон исключённого третьего, закон противоречия и закон достаточного основания.
В чем суть закона исключённого третьего?
Закон исключённого третьего гласит, что каждое утверждение может быть либо истинным (обозначает какое-либо утверждение), либо ложным (отрицает это утверждение), причем между этими двумя состояниями нет третьего варианта.